Building Blocks¶
The core of the motivation for the development of teili was to provide users
with a toolbox to easily build and combine neural BuildingBlocks which represent
basic algorithms implemented using neurons and synapses.
In order to provide these functionalities, all BuildingBlocks share the same
parent class which, amongst other things, provides I/O groups and properties to combine
BuildingBlocks hierarchically.
BuildingBlock¶
Every BuildingBlock has a set of parameters such as weights and refractory period, which can be specified outside the BuildingBlock``generation in a dictionary and are unpacked to the ``BuildingBlock upon creation..
Each BuildingBlock has the following attributes:
Attributes:
name (str, required): Name of the building_block population
neuron_eq_builder (class, optional): neuron class as imported from models/neuron_models
synapse_eq_builder (class, optional): synapse class as imported from models/synapse_models
params (dictionary, optional): Dictionary containing all relevant parameters for each building block
debug (bool, optional): Flag to gain additional information
groups (property): Class property to collect all keys to all neuron and synapse groups
monitors (dictionary): Keys to all spike and state monitors
monitor (bool, optional): Flag to auto-generate spike and state monitors
standalone_params (dictionary): Dictionary for all parameters to create a standalone network
sub_blocks (dictionary): Dictionary for all children building blocks
input_groups (dictionary): Dictionary containing all possible groups which are potential inputs
output_groups (dictionary): Dictionary containing all possible groups which are potential outputs
hidden_groups (dictionary): Dictionary containing all remaining groups which are neither inputs nor outputs
And as each BuildingBlock inherits from this parent class, all BuildingBlocks share the same attributes and properties.
To assure this every BuildingBlock initialises the BuildingBlock class:
BuildingBlock.__init__(self,
name,
neuron_eq_builder,
synapse_eq_builder,
block_params,
debug,
monitor)
Furthermore, as described above, as soon the parent class is initialised, each
BuildingBlock has a set of dictionaries which handle I/O to other Neuron and Connection groups or BuildingBlocks.
The BuildingBlock class comes with a set of __setter__ and __getter__ functions for collecting all groups involved or identifying a subset of groups which share the same tags
To retrieve all Neurons, Connections, SpikeGeneratorGroups etc. simply call the groups property:
test_wta= WTA(name='test_wta', dimensions=1, num_neurons=16, debug=False)
bb_groups = test_wta.groups
Tags¶
Each TeiliGroup has an attribute called _tags. The idea behind the _tags are that the user can easily define a dictionary and use this dictionary to obtain all TeiliGroups which share the same _tags.
Tags are defined as:
mismatch: (bool) Mismatch present of group
noise: (bool) Noise input, noise connection or noise presence
level: (int) Level of BuildingBlock in the hierarchy.
sign: (str : exc/inh/None) Sign on neuronal population. Follows Dale law.
target sign: (str : exc/inh/None) Sign of target population. None if not applicable.
num_inputs: (int) Number of inputs in Neuron population. None if not applicable.
bb_type: (str : WTA/ OCTA/ 3-WAY..) Building block type.
group_type: (str : Neuron/Connection/ SpikeGen) Group type
connection_type: (str : rec/lateral/fb/ff/None) Connection type
Setting Tags¶
Tags can be set using an entire dictionary. See tags for additional information.
test_wta = WTA(name='test_wta', dimensions=1, num_neurons=16, debug=False)
target_group = test_wta._groups['n_exc']
basic_tags_empty = {'mismatch' : 0,
'noise' : 0,
'level': 0 ,
'sign': 'None',
'target sign': 'None',
'num_inputs' : 0,
'bb_type' : 'None',
'group_type' : 'None',
'connection_type' : 'None',
}
test_wta._set_tags(basic_tags_empty, target_group)
and updated:
test_wta._tags['mismatch'] = True
Getting Tags¶
Specific groups can be filtered using specific tags:
test_wta.get_groups({'group_type': 'SpikeGenerator'})
All tags of a group can be obtained by:
test_wta.print_tags('n_exc')
Winner-takes-all (WTA)¶
For the WTA BuildingBlock the parameter dictionary looks as follows:
wta_params = {'we_inp_exc': 1.5,
'we_exc_inh': 1,
'wi_inh_exc': -1,
'we_exc_exc': 0.5,
'sigm': 3,
'rp_exc': 3 * ms,
'rp_inh': 1 * ms,
'ei_connection_probability': 1,
'ie_connection_probability': 1,
'ii_connection_probability': 0}
where each key is defined as:
we_inp_exc: Excitatory synaptic weight between input SpikeGenerator and excitatory neurons.
we_exc_inh: Excitatory synaptic weight between excitatory population and inhibitory interneuron.
wi_inh_exc: Inhibitory synaptic weight between inhibitory interneurons and excitatory population.
we_exc_exc: Self-excitatory synaptic weight.
wi_inh_inh: Self-inhibitory weight of the interneuron population.
sigm: Standard deviation in number of neurons for Gaussian connectivity kernel.
rp_exc: Refractory period of excitatory neurons.
rp_inh: Refractory period of inhibitory neurons.
ei_connection_probability: Excitatory to interneuron connectivity probability.
ie_connection_probability: Interneuron to excitatory connectivity probability
ii_connection_probability: Interneuron to Interneuron connectivity probability.
Now we can import the necessary modules and build our building block.
from teili.building_blocks.wta import WTA
from teili.models.neuron_models import DPI
1 Dimensional WTA¶
The WTA BuildingBlock comes in two slightly different versions. The versions only differ in the dimensionality of the WTA.
# The number of neurons in your WTA population.
# Note that this number is squared in the 2D WTA
num_neurons = 50
# The number of neurons which project to your WTA.
# Note that this number is squared in the 2D WTA
num_input_neurons = 50
my_wta = WTA(name='my_wta', dimensions=1,
neuron_eq_builder=DPI,
num_neurons=num_neurons, num_inh_neurons=int(num_neurons/4),
num_input_neurons=num_input_neurons, num_inputs=2,
block_params=wta_params,
monitor=True)
2 Dimensional WTA¶
To generate a 2-dimensional WTA population you can do the following:
# The number of neurons in your WTA population.
# Note that this number is squared in the 2D WTA
num_neurons = 7
# The number of neurons which project to your WTA.
# Note that this number is squared in the 2D WTA
num_input_neurons = 10
my_wta = WTA(name='my_wta', dimensions=2,
neuron_eq_builder=DPI,
num_neurons=num_neurons, num_inh_neurons=int(num_neurons**2/4),
num_input_neurons=num_input_neurons, num_inputs=2,
block_params=wta_params,
monitor=True)
Attention
The generation of the 2D WTA internally squares the number of neurons specified in num_neurons only for the excitatory population, not for the inhibitory population.
Changing a certain Connections group from being static to plastic:
from teili.core.groups import Connections
from teili.models.synapse_models import DPIstdp
my_wta._groups['s_exc_exc'] = Connections(my_wta._groups['n_exc'],
my_wta._groups['n_exc'],
equation_builder=DPIstdp
method='euler',
name=my_wta._groups['s_exc_exc'].name)
my_wta._groups['s_exc_exc'].connect(True)
Now we replaced the standard DPI synapse for the recurrent connection within a WTA population with an All-to-All STDP-based DPI synapse. In order to initialize the plastic weight w_plast we need to do:
my_wta._groups['s_exc_exc'].weight = 45
my_wta._groups['s_exc_exc'].namespace.update({'w_mean': 0.45})
my_wta._groups['s_exc_exc'].namespace.update({'w_std': 0.35})
# Initializing the plastic weight randomly
my_wta._groups['s_exc_exc'].w_plast = 'w_mean + randn() * w_std'
Chain¶
Note
TBA by Alpha Renner
Sequence learning¶
Note
TBA by Alpha Renner
Threeway network¶
Threeway block consists of three 1D WTA blocks and one 2D WTA,
thus no additional parameters are passed in the block_params dictionary, only the ones
needed to configure the WTA.
To initialize the block provide it with the connectivity pattern in the hidden layer and the cutoff setting used for all WTA blocks:
from teili.building_blocks.threeway import Threeway
from teili.tools.three_way_kernels import A_plus_B_equals_C
TW = Threeway('TestTW',
hidden_layer_gen_func = A_plus_B_equals_C,
cutoff = 2,
monitor=True)
Note
You always have to set monitor to True to be able to use the method get_values() to calculate the population vectors.
In addition to standard BuildingBlock arguments you can also specify these optional parameters:
num_input_neurons (int): Sizes of input/output populations A, B and C
num_hidden_neurons (int): Size of the hidden population H
hidden_layer_gen_func (function): A function providing connectivity pattern
A list of attributes available specific to the block:
A, B and C (WTA): Shortcuts for input/output 1d
WTAbuilding blocksH (WTA): A shortcut for the hidden population H implemented with a 2d
WTAbuilding blockInp_A, Inp_B, Inp_C (PoissonGroup): Shortcuts to input spike generators
value_a, value_b, value_c (double): Population vector values decoded with get_values() input for A, B and C
Threeway class also implements the following methods unique to the block:
set_A(float), set_B(float) and set_C(float): Sets spiking rates of neurons of the PoissonGroup
Inp_A,Inp_BandInp_C, respectively, to satisfy a shape of a gaussian bump centered at ‘value’ between 0 and 1reset_A(), reset_B() and reset_C(): Resets spiking rates of the neurons of the respective
PoissonGroups to zero (e.g. turns the inputs off)reset_inputs(): turns all three inputs off
get_values(ms): Extracts and updates encoded values of A, B and C from the spiking rates of the corresponding populations. Must be called to get the numerical results
plot(): calls a preconfigured instance of the
Visualizerto plot the raster for populations A, B and C
Online Clustering of Temporal Activity (OCTA)¶
Online Clustering of Temporal Activity (OCTA) is a second generation BuildingBlock:
it uses multiple WTA networks recurrently connected to create a cortex-inspired
microcircuit that, leveraging the spike timing
information, enables investigations of emergent network dynamics [1] (Download).
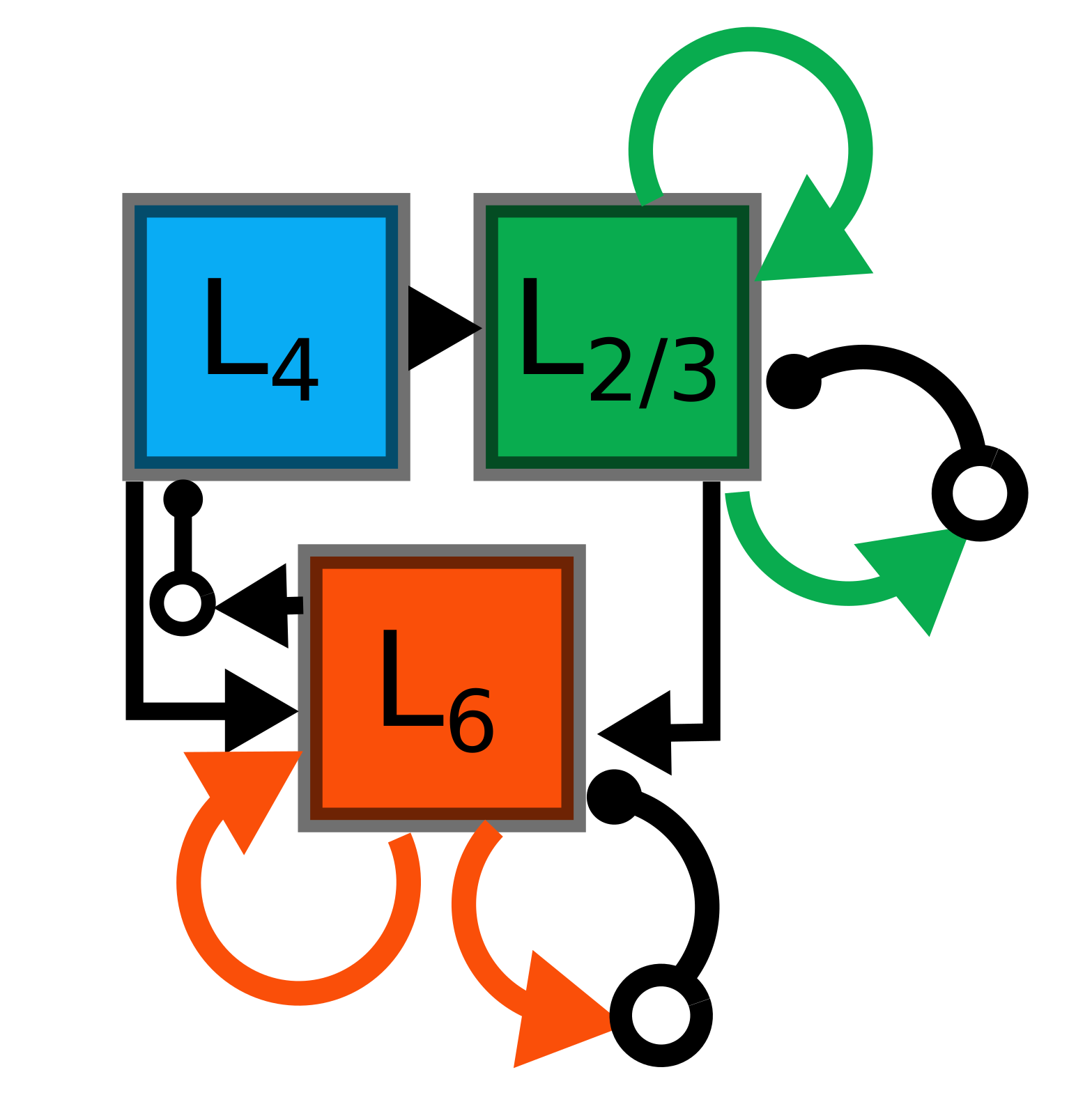
Schematic overview of a single OCTA BuildingBlock¶
The basic OCTA module consists of a projection (L4), a clustering (Layer2/3) and a prediction (L5/6) sub-module. Given that all connections are subject to learning, the objective of one OCTA module is to continuously adjust its parameters, e.g. synaptic weights and time constants, based on local information to best capture the spatio-temporal statistics of its input.
Parameters for the network are stored in two dictionaries located in tools/octa_tools/octa_params.py
The WTA keys are explained above, the OCTA keys are defined as:
duration (int): Duration of the simulation.
revolutions (int): Number of times input is presented.
num_neurons (int): Number of neurons in the compression WTA group. Keep in mind OCTA uses 2D WTAs.
num_input_neurons (int): Number of neurons in the projection and prediction WTA.
distribution (bool): Distribution from which to initialize the weights. Gamma (1) or normal (0) distributions.
dist_param_init (int): Shape for gamma distribution or mean of Gaussian distribution to be used at initialisation.
scale_init (int): Scale for gamma distribution or std of normal distribution.
dist_param_re_init (int): Shape of gamma distribution or mean of normal distribution used during the run regular functions.
scale_re_init (int): Scale for gamma distribution or std of normal distribution used during the run regular functions.
re_init_threshold (float): Parameter between 0 and 1.0. The weights gets reinitialized if the mean weight of a synapse is below the given value or above
1 - re_init_threshold.buffer_size_plast (int): Length of the buffer used by the activity dependent plasticity (ADP) mechanism. ADP acts as homeostatic regulariser.
noise_weight (int): Synaptic weight the PoissonSpikeGenerator which injects noise to the network.
variance_th_c (float): Variance threshold for the compression group. Parameter included in the
activitysynapse template used for ADP.variance_th_p (float): Variance threshold for the prediction group. Parameter included in the
activitysynapse template used for ADP.learning_rate (float): Learning rate.
inh_learning_rate (float): Inhibitory learning rate.
decay (int): Decay parameter of the decay in the activity dependent run_regular.
seed (int): Seed for mismatch. Default is 42.
tau_stdp (int): Time constant in ms that defines the STDP plasticty.
Initialisation of the building block goes as follows:
from brian2 import ms
from teili import TeiliNetwork
from teili.building_blocks.octa import Octa
from teili.models.parameters.octa_params import wta_params, octa_params
from teili.models.neuron_models import OCTA_Neuron as octa_neuron
from teili.stimuli.testbench import OCTA_Testbench
Net = TeiliNetwork()
OCTA = Octa(name='OCTA',
wta_params=wta_params,
octa_params=octa_params,
neuron_eq_builder=octa_neuron,
num_input_neurons=10,
num_neurons=7,
external_input=True,
noise=True,
monitor=True,
debug=False)
testbench_stim = OCTA_Testbench()
testbench_stim.rotating_bar(length=10, nrows=10,
direction='cw',
ts_offset=3, angle_step=10,
noise_probability=0.2,
repetitions=90,
debug=False)
OCTA_net.groups['spike_gen'].set_spikes(indices=testbench_stim.indices,
times=testbench_stim.times * ms)
Net.add(
OCTA_net,
OCTA_net.sub_blocks['prediction'],
OCTA_net.sub_blocks['compression']
)
Net.run(octa_params['duration']*ms, report='text')
Attention
When Neurons or Connections groups of a BuildingBlock are changed from their default, one needs to add the affected sub_blocks explicitly.
The additional keyword arguments are defined as:
external_input: Flag to include an input to the network
noise: Flag to include 10 Hz Poisson noise generator on
n_excof compression and predictionmonitor: Flag to return monitors of the network
debug: Flag for verbose debug
- 1
Milde, Moritz, PhD thesis, “Spike-Based Computational Primitives for Vision-Based Scene Understanding”, University of Zurich, 2019.